Two weeks ago I failed to get to a NZTA Secondary Teachers Reference Group Meeting in Wellington. I was running a workshop on citizenship and road safety education. After an over early start to catch the flight I spent the morning flying part way down the island before being turned back by fog at Wellington airport and returning to where I started from.
It was a morning spent “faffing around” at airports and in planes – but that is one of the expectations in the day job. Some days life behaves badly and refuses to apologise – you just have to get on with making something out of the rest of the day. The bonus is that I can share one of the reverse hexagons activities I prepared for the day.
HookED SOLO Reverse Hexagons.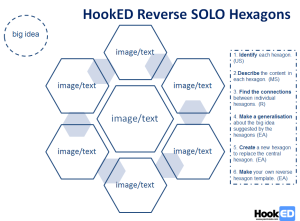
The SOLO Hexagons process can be usefully reversed in a “what’s the connection” thinking strategy –
Reverse Hexagons Strategy 1 – ask students to add annotations to an existing tessellation
Reverse Hexagons Strategy 2 – ask students to choose hexagons to fit a blank tessellation template with existing annotations. (more challenging) – For an example of this strategy used in maths see below
Reverse Hexagons Strategy 3 – ask students to make up their own SOLO Reverse Hexagons template
Note: The Moldiv app recommended by Jivespin blog is great for creating templates for images. Up till now I have been following a rather tortuous process on Photoshop.
Another example of HookED SOLO Reverse Hexagons is seen in the chapter on hexagons in the latest Essential Resources book on using SOLO when thinking like a mathematician. We had a lot of fun with the ideas and strategies in this book when I was working with the fabulous maths department at Kaipara College on Friday. Refer Figure 5.10: End of unit fraction sum up activity sheet page 40 in Hook, Gravett, Howard and John (2014)SOLO Taxonomy in Mathematics. Strategies for thinking like a mathematician
SOLO hexagons thinking is a “sandpit pedagogy”.
There are so many different contexts where making connections is a prompt for new learning that it is easy to forget SOLO hexagons are only one of many effective strategies for shifting the SOLO level of students’ thinking. “Over-hexagoning” students was a feature of the early adopters of SOLO in the UK where thinking with hexagons was often misrepresented as “doing SOLO”. It was of course nothing of the sort. But it can take awhile for the early adopter hype to settle. Hexagon thinking is based on an idea for “systems thinking” from AM Hodgson. (1992). Hexagons for systems thinking.European Journal of Systems Dynamics 59 (1): 220-30.
Putting the “hype” to one side, when used in measured ways, SOLO hexagons is a great way to introduce students of all ages to SOLO as a model of learning outcomes – loose ideas are important – connecting them in different ways makes them more interesting and shows more complex understanding. Sitting outside the clusters and asking – what is it all about? leads to conceptual understanding, big picture thinking and insight.
SOLO Hexagons can be used to determine a student’s depth of prior knowledge and understanding before starting to learn. They can also be used as a learning experience prompt to increase and deepen understanding, and to create new understanding by introducing hexagons with additional content – ideas, symbols, images etc.
Being a sandpit pedagogy means many different iterations have developed. I have posted examples of my favourites on the HookED wiki Effective Stategies Hexagons page. Reverse hexagons is one – there are many more.
{ 1 comment… read it below or add one }
You can also make them easily in google slides. You insert a photo into the document and then click crop on the toolbar. There is a small drop down menu with shapes, you then select the hexagon with a small 6 inside. This will crop your photo into a hexagon, then you repeat and move them into a giant hexagon.